Distributionally Robust Kalman Filter

(arXiv)

Minhyuk Jang, Astghik Hakobyan, Insoon Yang.

First two authors contributed equalliy.

Abstract

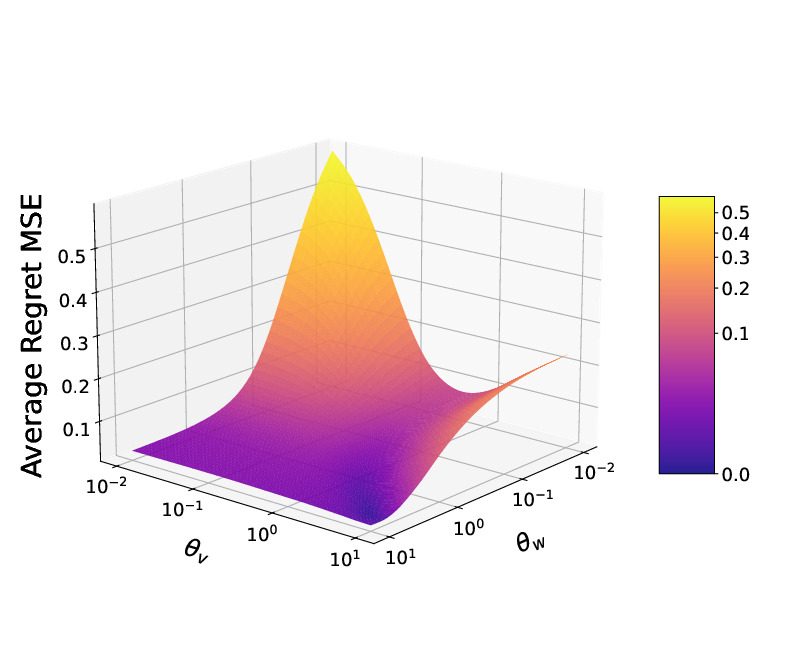
In this work, we propose a noise-centric formulation of the distributionally robust Kalman filter (DRKF) for discrete-time linear stochastic systems with uncertain noise statistics. By placing Wasserstein ambiguity sets directly on the process and measurement noise distributions, the proposed DRKF preserves the analytical structure of the classical Kalman filter while providing \emph{a priori} spectral bounds on all feasible covariances. In the time-invariant setting, we derive a steady-state DRKF from a single stationary semidefinite program, yielding a constant-gain estimator with the same per-step computational complexity as the standard Kalman filter. We establish conditions guaranteeing the existence, uniqueness, and convergence of this steady-state solution, and we prove its asymptotic minimax optimality with respect to the worst-case mean-square error. Numerical experiments validate the theory and demonstrate that the proposed DRKF improves estimation accuracy under unknown or uncertain noise models while offering computational advantages over existing robust and distributionally robust filters.